Física 1 UIP : Leyes de redondeo, uso de cifras significativas y notación cientifica

Método común

Las reglas del redondeo se aplican al decimal situado en la siguiente posición al número de decimales que se quiere transformar, es decir, si tenemos un número de 3 decimales y queremos redondear a la centésima, se aplicará las reglas de redondeo:

Dígito menor que 5: Si el siguiente decimal es menor que 5, el anterior no se modifica.

Ejemplo: 12,612. Redondeando a 2 decimales se debe tener en cuenta el tercer decimal: 12,612 ≈ 12,61.

Dígito mayor o igual que 5: Si el siguiente decimal es mayor o igual que 5, el anterior se incrementa en una unidad.

Ejemplo: 12,618. Redondeando a 2 decimales se debe tener en cuenta el tercer decimal: 12,618 ≈ 12,62
Ejemplo: 2,3571 redondeado a la centésima es 2,36 , debido a que 2,3571 está más cerca de 2.36 que de 2.35.

"Se no hace mas sencillo manejar una cifra mas pequeña y

fácil de manipular"

Utilizar correctamente el redondeo y las cifras significativas para aproximar los resultados

1. Cualquier dígito diferente de cero es significativo.

1234.56 6 cifras significativas

2. Ceros entre dígitos distintos de cero son significativos.

1002.5 5 cifras significativas

3. Ceros a la izquierda del primer dígito distinto de cero no son significativos.

000456 3 cifras significativas

0.0056 2 cifras significativas

4. Si el número es mayor que (1), todos los ceros a la derecha del punto decimal son significativos.

457.12 5 cifras significativas

400.00 5 cifras significativas

5. Si el número es menor que uno, entonces únicamente los ceros que están al final del número y entre los dígitos distintos de cero son significativos.

0.01020 4 cifras significativas

6. Para los números que contengan puntos decimales, los ceros que se arrastran pueden o no pueden ser significativos.

1,000 1, 2, 3, o 4 cifras significativas. Supondremos 4 en nuestros cálculos

0.0010 2 cifras significativas

1.000 4 cifras significativas

7. Supondremos que cantidades definidas o contadas tienen un número ilimitado de cifras significativas

NOTA: Es mucho más fácil contar y encontrar las cifras significativas si el número está escrita en notación significativa.

Uso en cálculos

1. Suma y Sustracción: El número de cifras significativas a la derecha del punto decimal en la suma o la diferencia es determinada por el número con menos cifras significativas a la derecha del punto decimal de cualquiera de los números originales.

6.2456 + 6.2 = 12.4456 redondeado a 12.4

nota: 3 cifras significativas en la respuesta

2. Multiplicación y División: El número de cifras significativas en el producto final o en el cociente es determinado por el número original que tenga las cifras significativas más pequeño.

2.51 x 2.30 = 5.773 redondeada a 5.77

2.4 x 0.000673 = 0.0016152 redondeado a 0.0016

Redondeando

1. Aumente en uno al dígito que sigue a la última cifra significativa si el primer dígito es menor que 5.

Redondear 1.61562 a 2 cifras significativas RESP: 1.6

2. Si el primer dígito a truncar es mayor que cinco, incrementar el dígito precedente en 1.

Redondear 1.61562 a 5 cifras significativas RESP: 1.6156

3. Si el primer dígito a truncar es cinco y hay dígitos diferentes de cero después del cinco, incrementa el dígito precedente en 1.

Redondear 1.61562 a 3 cifras significativas RESP: 1.62

Redondear 1.62500003 a 3 cifras significativas RESP: 1.63

4. Si el primer dígito a truncar es cinco y hay únicamente ceros después del cinco, redondee al número par.

Redondear 1.655000 a 3 cifras significativas Resp: 1.66

La notación científica (o notación índice estándar) es una manera rápida de representar un número utilizando potencias de base diez. Esta notación se utiliza para poder expresar muy fácilmente números muy grandes o muy pequeños.

Los números se escriben como un producto:

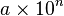
$a \times 10^n\,$